各Labの記録
まえがき
Qiskit Global Summer School 2023 Lab5の記録です。
Lab 5: Error mitigation with Qiskit Runtime
エラー緩和(Error mitigation)をするラボ。
具体的には、単純な観測値と初期状態を定義し、Estimatorプリミティブを使って期待値を測定する。
ノイズの多いシミュレーションを用いて、さまざまなエラー緩和戦略の効果を探る。
Setup
例として簡単なハイゼンベルグ ・ハミルトニアン ・モデルを定義する。また、簡単な状態準備回路を構築する。
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.quantum_info import SparsePauliOp
def heisenberg_hamiltonian (
length: int , jx: float = 1.0 , jy: float = 0.0 , jz: float = 0.0
) -> SparsePauliOp:
terms = []
for i in range (length - 1 ):
if jx:
terms.append(("XX" , [i, i + 1 ], jx))
if jy:
terms.append(("YY" , [i, i + 1 ], jy))
if jz:
terms.append(("ZZ" , [i, i + 1 ], jz))
return SparsePauliOp.from_sparse_list(terms, num_qubits=length)
def state_prep_circuit (num_qubits: int , layers: int = 1 ) -> QuantumCircuit:
qubits = QuantumRegister(num_qubits, name="q" )
circuit = QuantumCircuit(qubits)
circuit.h(qubits)
for _ in range (layers):
for i in range (0 , num_qubits - 1 , 2 ):
circuit.cx(qubits[i], qubits[i + 1 ])
circuit.ry(0.1 , qubits)
for i in range (1 , num_qubits - 1 , 2 ):
circuit.cx(qubits[i], qubits[i + 1 ])
circuit.ry(0.1 , qubits)
return circuit
length = 5
hamiltonian = heisenberg_hamiltonian(length, 1.0 , 1.0 )
circuit = state_prep_circuit(length, layers=2 )
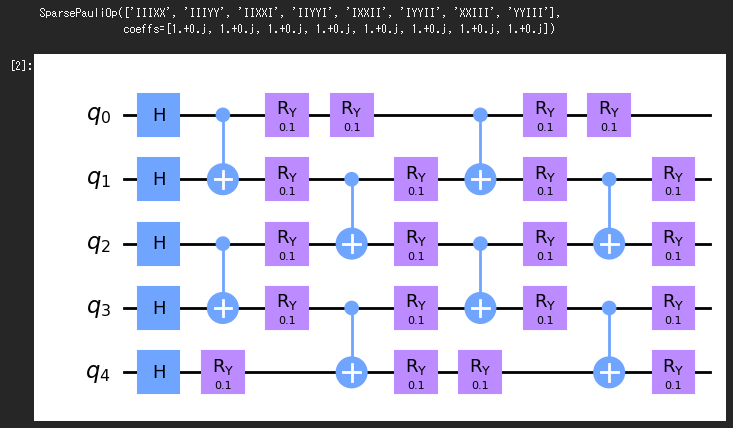
print (hamiltonian)
circuit.draw("mpl" )
ハミルトニアン と準備回路
Calculate exact expectation value (energy)(翻訳)
まず、Estimatorプリミティブのローカルシミュレータ実装を使って正確な期待値を計算する。ハミルトニアン の期待値は "エネルギー "とも呼ばれる。
from qiskit_aer.primitives import Estimator
estimator = Estimator(approximation=True )
job = estimator.run(circuit, hamiltonian, shots=None )
result = job.result()
exact_value = result.values[0 ]
print (f"Exact energy: {exact_value}" )
Run noisy simulation through Qiskit Runtime
次に、Qiskit Runtimeサービスを初期化し、ノイズを扱えるシミュレータに支えられたEstimatorプリミティブの使用に切り替える。この回路は5量子ビット で動作するが、量子ビット 選択の潜在的 な効果を後で示すために、6量子ビット でシミュレータを初期化する。
from qiskit_ibm_runtime import QiskitRuntimeService
hub = "ibm-q-internal"
group = "deployed"
project = "default"
service = QiskitRuntimeService(instance=f"{hub}/{group}/{project}" )
from qiskit_ibm_runtime import Estimator, Options, Session
from qiskit.transpiler import CouplingMap
backend = service.get_backend("simulator_statevector" )
simulator = {
"basis_gates" : ["id" , "rz" , "sx" , "cx" , "reset" ],
"coupling_map" : list (CouplingMap.from_line(length + 1 )),
}
shots = 10000
No noise
まずはノイズなしのシミュレータで実行してみる。
from qiskit_ibm_runtime import Estimator, Options, Session
from qiskit.transpiler import CouplingMap
import math
options = Options(
simulator=simulator,
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 4.275399999999999
Energy error: 0.015538711029713603
Variance: 4.44106724
Standard error: 0.021073839801991474
誤差(Energy error)が 0.015... という値になった。ノイズなしでこのくらいになると覚えておいて、以下を進めていこう。
Readout error
次に、Readout error(読み出しエラー)ありのシミュレータで実行してみる。
ex1
この課題では、本当に悪い Readout error を持つ最初の量子ビット を除いたすべての量子ビット のReadout errorが緩やかなノイズモデルを構築する。
具体的には、以下の特性を持つノイズモデルを構築すること:
q0
50%の確率で1を0と読み間違える
20%の確率で0を1と読み間違える
それ以外の量子ビット
5%の確率で1を0と読み間違える
2%の確率で0を1と読み間違える
ノイズ作るライブラリは以下たちを参照すると良い。
from qiskit_aer.noise import NoiseModel, ReadoutError
noise_model = NoiseModel()
rest_p0given1 = 0.05
rest_p1given0 = 0.02
rest_readout_error = ReadoutError([[1 - rest_p1given0, rest_p1given0], [rest_p0given1, 1 - rest_p0given1]])
noise_model.add_all_qubit_readout_error(rest_readout_error)
q0_p0given1 = 0.5
q0_p1given0 = 0.2
q0_readout_error = ReadoutError([[1 - q0_p1given0, q0_p1given0], [q0_p0given1, 1 - q0_p0given1]])
noise_model.add_readout_error(q0_readout_error, (0 ,))
print (noise_model)
WARNING: Specific readout error on qubits (0,) overrides previously defined all-qubit readout error for these qubits.
NoiseModel:
Basis gates: ['cx', 'id', 'rz', 'sx']
Instructions with noise: ['measure']
Qubits with noise: [0]
All-qubits errors: ['measure']
Specific qubit errors: [('measure', (0,))]
まず、読み出しエラーを緩和するために何もせずにシミュレーションを実行してみる。明示的にresilience_level = 0を設定し、Runtimeサービスによるエラー緩和が適用されないようにする。不適切な量子ビット の選択の影響を説明するために、量子ビット 0を含む初期レイアウトを明示的に指定する。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
transpilation=dict (initial_layout=list (range (length))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 3.5386
Energy error: 0.7523387110297128
Variance: 5.337599239999999
Standard error: 0.023103244880319302
この誤差(Energy error)はかなり大きい。これを改善するために、量子ビット 0を避けるような量子ビット レイアウトを選んでみよう。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
transpilation=dict (initial_layout=list (range (1 , length + 1 ))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 3.9506
Energy error: 0.3403387110297129
Variance: 4.962461319999999
Standard error: 0.02227658259248936
誤差(Energy error)は小さくなったが、それでもまだ大きい。resilience_level = 1に設定して、読み出しエラー緩和を有効にしてみよう。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=1 ,
transpilation=dict (initial_layout=list (range (1 , length + 1 ))),
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 4.303468384959293
Energy error: 0.012529673929580376
Variance: 7.169951196036428
Standard error: 0.02677676454696577
誤差(Energy error)はかなり小さくなり、読み出しエラーの影響はほぼ完全に緩和されたことがわかった。この緩和は「タダ」ではない。特に、
読み出しエラーを緩和するために、ランタイムサービスは追加のキャリブレーション 回路を実行する必要があるため、全体的な実行時間が長くなる可能性がある。
推定値の分散が大きくなり、平均値の標準誤差が大きくなる。その結果、所定の標準誤差を達成するためには、より多くのショットを指定する必要がある。
通常このようなコストは比較的小さいため、読み出しエラーの緩和を可能にすることは、ほとんどの場合、価値がある。
ex2
読み出しエラーの緩和をオンにすると、推定値の分散(Variance)が2倍増加すると仮定する。
元々10,000ショットで実験を行った場合、平均の標準誤差(Standard error)を同じにするためには今何ショットを使用すべきか?
bellcurve.jp
元々標準偏差 を
読み出しエラーの緩和をオンにしたときのショット数を標準偏差 を
読み出しエラーの緩和をオンにすると分散が2倍になるので、標準偏差 は
標準誤差
new_shots: int
new_shots = 20000
Depolarizing error and zero-noise extrapolation
このセクションでは、ゼロノイズ外挿(zero-noise extrapolation)を使ってどのように脱分極エラー(depolarizing error)を軽減できるかを見ていく。Qiskit Runtimeのゼロノイズ外挿機能はまだベータ版であるため、現在いくつかの制限がある。
特に、本稿執筆時点では、ゼロノイズ外挿機能は読み出しエラーを緩和しない。
したがって以下の例では、ノイズモデルから読み出しエラーを取り除く。
ex3
各CNOTゲートの後に2量子ビット の脱分極エラーを加えるノイズモデルを構築し、エラーチャネルが1%の確率で入力量子状態を完全混合状態にマップするようにする。
qiskit.org
depolarizing_error
第1引数:確率
第2引数:n-qubit用の脱分極エラーかを指定する
今回CNOTゲートは2-qubitゲートなので、第2引数は2を指定する。
詳しい使い方はNoise Models (qiskit_aer.noise) の「Example: depolarizing noise model」に書いてある。
from qiskit_aer.noise import depolarizing_error
noise_model = NoiseModel()
depolar_p = 0.01
depolar_error = depolarizing_error(depolar_p, 2 )
noise_model.add_all_qubit_quantum_error(depolar_error, ['cx' ])
print (noise_model)
NoiseModel:
Basis gates: ['cx', 'id', 'rz', 'sx']
Instructions with noise: ['cx']
All-qubits errors: ['cx']
resilience_level = 0でestimatorを実行してみる。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 4.0624
Energy error: 0.2285387110297128
Variance: 4.79633856
Standard error: 0.021900544650761543
次はresilience_level = 1で読み出しエラーの緩和をオンにしてestimatorを実行してみよう。今このノイズモデルには読み出しエラーの緩和は含まれていないため、これによる効果は期待できない。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=1 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 4.0586
Energy error: 0.23233871102971282
Variance: 4.8106246
Standard error: 0.02193313611866757
予想通り、resilience_level = 0のときと誤差(Energy error)は変わらない結果となった。
では、resilience_level = 2に設定して、ゼロノイズ外挿をオンにして実行してみよう。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 4.206533333333335
Energy error: 0.08440537769637846
Variances: [4.84564196, 5.46333092, 5.91612628]
Standard error: [0.022012818901721787, 0.02337376931519604, 0.024323088372984216]
誤差(Energy error)がかなり小さくなったことがわかる。脱分極ノイズの影響はほぼ完全に緩和されたおかげである。
推定量 に対する単一の分散値を得る代わりに、外挿のために測定された各データポイントに対する分散のリストを返すようになったことに注意。Qiskit Runtimeの将来のバージョンでは、これらの分散も外挿され、最終的な推定量 に対して単一の分散が返されるようになるだろう。
ex4(ungraded)
脱分極エラー(depolarizing error)以外に、どのような種類のノイズがゼロノイズ外挿によって緩和できるだろうか?他のノイズモデルを構築し、ゼロノイズ外挿を使った場合と使わない場合でシミュレーションを行い、あなたの提案をテストしてみよ。
Noise Models (qiskit_aer.noise) の「Quantum Error Functions」の項目に色々エラーの種類が書いてある。
以下の記事を大いに参考にした。
Coherent Noiseをrx,ry,rzゲートに使ってみる。
from qiskit_aer.noise import coherent_unitary_error
from qiskit.circuit.library import RYGate, RXGate, RZGate
noise_model = NoiseModel()
epsilon = math.pi/30
epsilon_rotation = RYGate(epsilon).to_matrix()
over_rotation = coherent_unitary_error(epsilon_rotation)
noise_model.add_all_qubit_quantum_error(over_rotation, ['ry' ])
epsilon_rotation = RXGate(epsilon).to_matrix()
over_rotation = coherent_unitary_error(epsilon_rotation)
noise_model.add_all_qubit_quantum_error(over_rotation, ['rx' ])
epsilon_rotation = RZGate(epsilon).to_matrix()
over_rotation = coherent_unitary_error(epsilon_rotation)
noise_model.add_all_qubit_quantum_error(over_rotation, ['rz' ])
print (noise_model)
NoiseModel:
Basis gates: ['cx', 'id', 'rx', 'ry', 'rz', 'sx']
Instructions with noise: ['ry', 'rx', 'rz']
All-qubits errors: ['ry', 'rx', 'rz']
まずはresilience_level = 0で実行。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 3.9776
Energy error: 0.3133387110297132
Variance: 4.8817328
Standard error: 0.02209464369479626
次にresilience_level = 2で実行。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 3.6169500000000014
Energy error: 0.6739887110297116
Variances: [5.236187, 5.256725159999999, 5.26025432]
Standard error: [0.022882716184928747, 0.02292754928028724, 0.02293524431960558]
ゼロノイズ外挿によって緩和しなかった。というか誤差(Energy error)がひどくなってる。
pauli_errorをid,rx,ry,rzゲートに使ってみる
ある確率でbit-flipエラーやphase-flipエラーを起こすノイズを追加する。
from qiskit_aer.noise import pauli_error
p_error = 0.01
bit_flip_error = pauli_error([('X' , p_error), ('I' , 1 - p_error)])
phase_flip_error = pauli_error([('Z' , p_error), ('I' , 1 - p_error)])
noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(bit_flip_error, ['id' , "rx" , "ry" , "rz" ])
noise_model.add_all_qubit_quantum_error(phase_flip_error, ['id' , "rx" , "ry" , "rz" ])
print (noise_model)
WARNING: all-qubit error already exists for instruction "id", composing with additional error.
WARNING: all-qubit error already exists for instruction "rx", composing with additional error.
WARNING: all-qubit error already exists for instruction "ry", composing with additional error.
WARNING: all-qubit error already exists for instruction "rz", composing with additional error.
NoiseModel:
Basis gates: ['cx', 'id', 'rx', 'ry', 'rz', 'sx']
Instructions with noise: ['ry', 'id', 'rx', 'rz']
All-qubits errors: ['id', 'rx', 'ry', 'rz']
まずはresilience_level = 0で実行。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 2.5622
Energy error: 1.7287387110297132
Variance: 6.7096326
Standard error: 0.025902958518285127
次にresilience_level = 2で実行。
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 2.467666666666668
Energy error: 1.823272044363045
Variances: [6.82206672, 6.840397360000001, 6.86765392]
Standard error: [0.02611908635461815, 0.026154153322178107, 0.026206209035264907]
ゼロノイズ外挿によって緩和しなかった。
thermal_relaxation_error(熱緩和エラー)をid,rx,ry,rzゲートに使ってみる
from qiskit_aer.noise import thermal_relaxation_error
t_error = thermal_relaxation_error(161.83e3 , 61.64e3 , 368 )
noise_model = NoiseModel()
noise_model.add_all_qubit_quantum_error(t_error, ['id' , "rx" , "ry" , "rz" ])
print (noise_model)
resilience_level = 0で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 3.908
Energy error: 0.3829387110297131
Variance: 5.06420016
Standard error: 0.022503777816180112
resilience_level = 2で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 3.8287833333333356
Energy error: 0.4621553776963774
Variances: [5.20887776, 5.223925960000001, 5.2486150799999995]
Standard error: [0.022822965977278238, 0.022855909432792212, 0.022909856132241425]
エラー緩和しなかった。
thermal_relaxation_error(熱緩和エラー)をCNOTゲートに使ってみる
今までrxゲートなどにノイズをのせていたが、よくよく考えたらLabではCNOTゲートにノイズを乗せていたのであった。なのでそうしてみる。
import numpy as np
qn = 5
T1s = np.random.normal(50e3 , 10e3 , qn)
T2s = np.random.normal(70e3 , 10e3 , qn)
T2s = np.array([min (T2s[j], 2 * T1s[j]) for j in range (qn)])
time_u1 = 0
time_u2 = 50
time_u3 = 100
time_cx = 300
time_reset = 1000
time_measure = 1000
errors_reset = [thermal_relaxation_error(t1, t2, time_reset)
for t1, t2 in zip (T1s, T2s)]
errors_measure = [thermal_relaxation_error(t1, t2, time_measure)
for t1, t2 in zip (T1s, T2s)]
errors_u1 = [thermal_relaxation_error(t1, t2, time_u1)
for t1, t2 in zip (T1s, T2s)]
errors_u2 = [thermal_relaxation_error(t1, t2, time_u2)
for t1, t2 in zip (T1s, T2s)]
errors_u3 = [thermal_relaxation_error(t1, t2, time_u3)
for t1, t2 in zip (T1s, T2s)]
errors_cx = [[thermal_relaxation_error(t1a, t2a, time_cx).expand(
thermal_relaxation_error(t1b, t2b, time_cx))
for t1a, t2a in zip (T1s, T2s)]
for t1b, t2b in zip (T1s, T2s)]
print (errors_cx)
[[QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c674160>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c91ad10>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c91bf70>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c675360>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c91b130>, 1.0)])], [QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7827d0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c780ac0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c783b50>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c781ab0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7819c0>, 1.0)])], [QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c91ace0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c675e70>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c783d00>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7830d0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7808b0>, 1.0)])], [QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c783dc0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c783550>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c781e40>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7832b0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c783310>, 1.0)])], [QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c782ce0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c780f10>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c780fa0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff68c7801c0>, 1.0)]), QuantumError([(<qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7ff6a8cae230>, 1.0)])]]
noise_model = NoiseModel()
for j in range (4 ):
for k in range (4 ):
noise_model.add_quantum_error(errors_cx[j][k], "cx" , [j, k])
resilience_level = 0で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
resilience_level = 2で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 4.286916666666666
Energy error: 0.004022044363047428
Variances: [4.57962836, 4.97150324, 5.158112879999999]
Standard error: [0.02140006626157966, 0.022296868031183213, 0.022711479212063665]
エラー緩和した 。ゼロノイズ外挿はCNOTゲートにしか効かない……?知識不足でわからない。
Coherent NoiseをCNOTゲートに使ってみる
from qiskit_aer.noise import coherent_unitary_error
from qiskit.circuit.library import RYGate, RXGate, RZGate, CUGate
noise_model = NoiseModel()
epsilon = math.pi/30
epsilon_rotation = CUGate(epsilon, epsilon, epsilon, epsilon).to_matrix()
over_rotation = coherent_unitary_error(epsilon_rotation)
noise_model.add_all_qubit_quantum_error(over_rotation, ['cx' ])
print (noise_model)
NoiseModel:
Basis gates: ['cx', 'id', 'rz', 'sx']
Instructions with noise: ['cx']
All-qubits errors: ['cx']
resilience_level = 0で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=0 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variance = result.metadata[0 ]["variance" ]
std = math.sqrt(variance / shots)
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variance: {variance}" )
print (f"Standard error: {std}" )
Estimated energy: 3.9168000000000003
Energy error: 0.37413871102971274
Variance: 5.076300159999999
Standard error: 0.02253064615140897
resilience_level = 2で実行
options = Options(
simulator=dict (noise_model=noise_model, **simulator),
resilience_level=2 ,
)
with Session(service=service, backend=backend):
estimator = Estimator(options=options)
job = estimator.run(circuit, hamiltonian, shots=shots)
result = job.result()
experiment_value = result.values[0 ]
error = abs (experiment_value - exact_value)
variances = result.metadata[0 ]["zne" ]["noise_amplification" ]["variance" ]
std = [math.sqrt(var/shots) for var in variances]
print (f"Estimated energy: {experiment_value}" )
print (f"Energy error: {error}" )
print (f"Variances: {variances}" )
print (f"Standard error: {std}" )
Estimated energy: 4.7794000000000025
Energy error: 0.4884612889702895
Variances: [5.0520554, 6.75144548, 7.730010119999999]
Standard error: [0.022476777793981058, 0.025983543792177387, 0.02780289574846476]
エラー緩和しなかった。これはCUGate使ってるのが間違ってそう。でもうーん、わからん。